| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- 정적 팩토리 메서드 패턴
- kruskal 알고리즘
- 이진탐색트리
- force=true
- @version
- max lifetime
- BST
- NoArgsConstructor
- JPA
- 후위 표기법
- binary search
- prim 알고리즘
- 비관적 락
- static factory method pattern
- 쿼리메소드
- query methods
- quick-sort
- 최대 유휴 시간
- 알고리즘
- 프로세스의 상태
- merge-sort
- 낙관적 락
- 중위 표기법
- 최대 유지 시간
- 트리
- disjoint-sets
- max idle time
- 프로세스
- 자료구조
- jparepository
- Today
- Total
Dionysus
[알고리즘🧩] 이진 탐색 (Binary Search) 본문
목차
💬 순차 탐색 (Sequential Search)
💬 이진 탐색 : 반으로 쪼개면서 탐색하기
💬 트리 자료구조
💬 이진 탐색 트리 (Binary Search Tree)
💬 연습문제
💬 순차 탐색 (Sequential Search)
배열 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 차례대로 확인하는 방법
- 정렬되지 않은 배열에서 데이터를 찾아야 할 때 주로 사용함
- 구현이 간단하다는 장점이 있음
- 데이터가 아무리 많아도 시간만 충분하다면 항상 원하는 데이터를 찾아낼 수 있다는 장점 있음
- 시간 복잡도: O(N)
💬 이진 탐색 : 반으로 쪼개면서 탐색하기
이진 탐색(Binary Search)은 배열 내부 데이터가 정렬되어 있어야만 사용할 수 있는 알고리즘으로, 찾으려는 데이터와 중간점(middle) 위치에 있는 데이터를 반복적으로 비교하여 원하는 데이터를 찾음
"이진 탐색은 코딩 테스트에서 단골로 나오는 문제이니 가급적 외우길 권한다." - 나동빈
- 배열이 이미 정렬되어 있다면 빠르게 데이터를 찾을 수 있다는 특징이 있음.
- 탐색 범위가 큰 상황에서 많이 사용됨 (처리해야 할 데이터의 개수가 1000만 단위 이상이 될 경우 이진탐색!!)
- 사용되는 변수 3가지
- 시작점, 끝점, 중간점
- 한 번 탐색할 때마다 확인하는 원소의 개수가 절반씩 줄어든다는 점에서 퀵 정렬과 공통점 있음
- 시간 복잡도: O(logN)
✔ 구현
- 재귀 함수로 구현
# 이진 탐색 소스코드 구현(재귀 함수)
def binary_search(array, target, start, end):
if start > end:
return None
mid = (start + end) // 2
# 찾은 경우 중간점 인덱스를 반환함
if array[mid] == target:
return mid
# 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽을 확인함
elif array[mid] > target:
return binary_search(array, target, start, mid - 1)
# 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽을 확인함
else:
return binary_search(array, target, mid + 1, end)
# N(원소의 개수)와 target(찾고자 하는 문자열)을 입력받음
N, target = list(map(int, input().split()))
# 전체 원소 입력받기
array = list(map(int, input().split()))
# 이진 탐색 수행 결과 출력
result = binary_search(array, target, 0, N - 1)
if result == None:
print("원소가 존재하지 않습니다.")
else:
print(result + 1)
# 출처: <이것이 취업을 위한 코딩 테스트다 - 나동빈>
- 반복문으로 구현
# 이진 탐색 소스코드 구현(반복문)
def binary_search(array, target, start, end):
while start <= end:
mid = (start + end) // 2
# 찾은 경우, 중간점 인덱스를 반환함
if array[mid] == target:
return mid
# 중간점의 값보다 찾고자 하는 값이 작은 경우, 왼쪽을 확인함
elif array[mid] > target:
end = mid - 1
# 중간점의 값보다 찾고자 하는 값이 큰 경우, 오른쪽을 확인함
start = mid + 1
return None
# N(원소의 개수)과 target(찾고자 하는 문자열)을 입력받음
N, target = list(map(int, input().split()))
# 전체 원소 입력받기
array = list(map(int, input().split()))
# 이진 탐색 수행 결과 출력
result = binary_search(array, target, 0, N - 1)
if result == None:
print("원소가 존재하지 않습니다.")
else:
print(result + 1)
# 출처: <이것이 취업을 위한 코딩 테스트다 - 나동빈>
💬 트리 자료구조
[자료구조🧬] 트리(Tree)
목차💬 트리(Tree)💬 이진 트리(Binary Tree)💬 이진 트리 - 순회(traversal)💬 이진 트리의 표현💬 이진 트리의 표현 코드💬 힙(Heap)💬 연습문제 💬 트리(Tree)더보기비선형 구조로, 원소들 간에 1:n
dionysaurus.tistory.com
💬 이진 탐색 트리 (Binary Search Tree, BST)
데이터들을 빠르게 검색할 수 있도록 체계적으로 저장해두고, 최대 O(log n)의 빠른 속도로 값을 검색할 수 있는 자료구조로, 특정 규칙을 갖는 이진트리 형태로 값을 저장한다.
(Python 공식 Library에는 BST(이진 탐색 트리) 자료구조가 내장되어 있지 않아 직접 구현해서 사용해야 함 → set 활용)
- 탐색 작업을 효율적으로 하기 위한 자료구조이다.
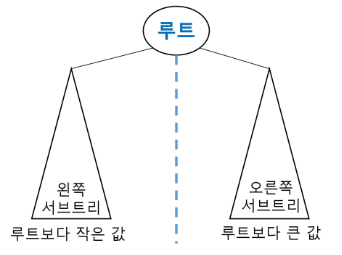
- 모든 원소는 서로 다른 유일한 키 값을 가지며, (왼쪽 서브트리의 key) < (루트의 key) < (오른쪽 서브트리의 key)의 관계를 가진다.
- 왼쪽 서브트리(subtree)와 오른쪽 서브트리(subtree)도 이진 탐색 트리이다.
- 중위 순회하면 오름차순으로 정렬된 값을 얻을 수 있다.
- 힙의 키를 우선순위로 활용하여 우선순위 큐를 구현할 수 있다.
⚡ 리스트 vs BST
# 리스트 성능
- 삽입: O(n), 단 맨 끝 삽입은 O(1)
- 삭제: O(n), 단 맨 끝 삭제는 O(1)
- 탐색: O(n)
# BTS 성능
- 삽입, 삭제, 탐색: 평균 O(logN)
▶ BST는 리스트보다 더 빠른 삽입 / 삭제 / 탐색이 가능함
✅ BST 삽입(insert) 연산
- 첫 번째 값은 root에 저장됨
- 비교할 노드 값보다 target 값이 더 큰 경우, 우측 자식 노드로 배정되며 그렇지 않으면 왼쪽 자식 노드로 배정됨
▶ 삽입(insert)을 위해 탐색 연산을 먼저 수행하여 트리에 같은 원소가 존재하는지를 확인한다.
▶ 탐색에서 탐색 실패가 결정되는 위치가 삽입 위치가 된다.
▷삽입을 위해 root에서부터 탐색하여 자기 위치를 찾는 데에 트리의 높이(h)만큼의 탐색 시간이 소요됨
▷ 따라서 완벽하게 균형 잡힌 이진트리의 경우, 삽입 시간복잡도는 O(logN)임

값을 비교하여 적절한 위치에 노드를 배치하는 과정
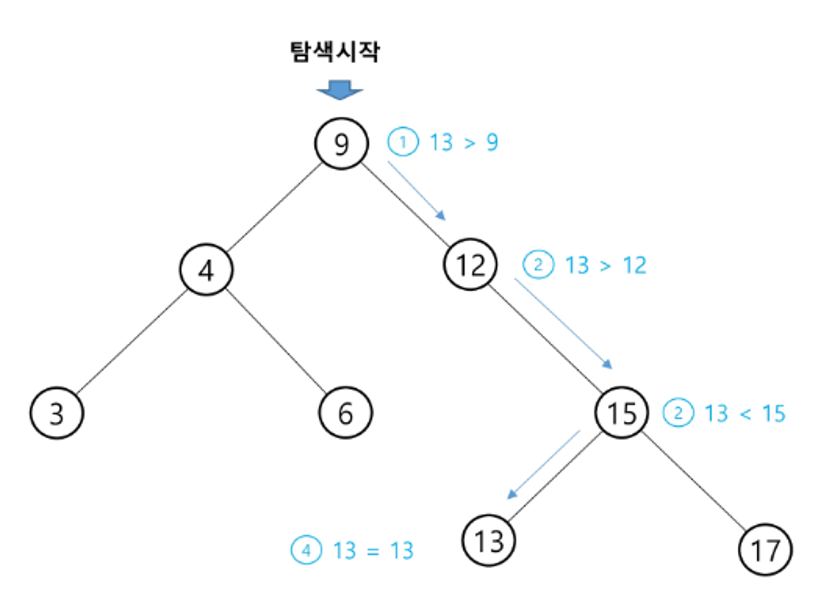
✅ BST 탐색(search) 연산
크기가 큰 값은 부모 노드의 우측에, 크기가 작은 값은 부모 노드의 좌측에 위치함을 활용하여 탐색함
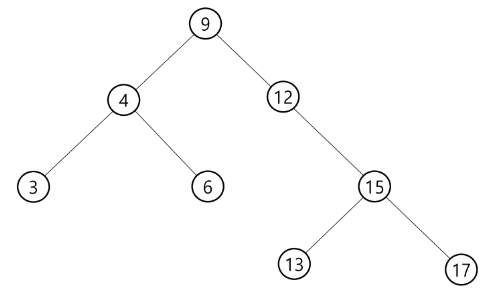
✅ BST 삭제(delete) 연산
아래의 트리에 대해 13, 12, 9를 차례로 삭제해본다.


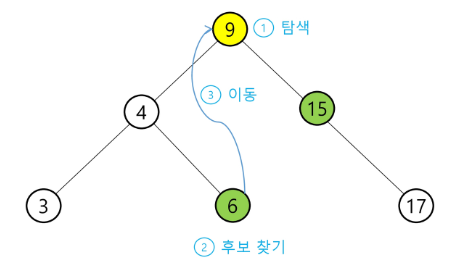
- 9를 삭제하는 경우, root 자리가 비어 있으므로 왼쪽 subtree에서 가장 큰 값인 6과 오른쪽 subtree에서 가장 작은 값인 12 둘 중 하나를 root 자리로 이동시킬 수 있다.
✅ BST - 연산의 시간복잡도
- 탐색(searching) / 삽입(insertion) / 삭제(deletion) 시간은 트리의 높이(h)만큼 시간이 걸린다.
- O(h), h: BST의 깊이
- 평균 시간 복잡도
- 이진 트리가 균형적으로 생성되어 있는 경우 → O(log n)
- 이진 트리가 균형적으로 생성되어 있는 경우 → O(log n)
- 최악의 시간 복잡도
- 한쪽으로 치우친 경사 이진 트리의 경우 → O(n)
(순차 탐색과 시간복잡도가 같음)
- 한쪽으로 치우친 경사 이진 트리의 경우 → O(n)
💬 연습문제
1. [BST] BST에서 DFS 중위순회를 한다면 Key 값이 작은 순서대로 탐색이 가능하다. 이를 설명하시오.
- 중위 순회의 쉬운 이해: 편지 전달
각 노드는 아래 세 가지 미션을 순서대로 수행해야 한다.- 왼쪽 노드로 편지를 즉시 전달함
- 왼쪽 노드로부터 편지를 돌려받는다면, 편지를 읽음 (탐색함)
- 편지를 읽은 후에는, 오른쪽 노드로 편지를 전달함
(단, dummy 노드는 편지를 받자마자 즉시 돌려준다. 또한 위 세 가지 미션을 모두 수행한 노드는 상위 노드에게 편지를 되돌려준다.)

'CS 및 알고리즘 공부 > 알고리즘' 카테고리의 다른 글
| [알고리즘🧩] 완전 검색 / 탐욕 알고리즘 (2) | 2024.09.03 |
|---|---|
| [알고리즘🧩] 큐 (Queue) (0) | 2024.08.13 |
| [알고리즘🧩] Stack (0) | 2024.08.10 |




